Learning Goals:
- Understand function notation.
- Understand how to find the domain and range of a function.
Today I discussed how to describe functions using function notation. The symbol:
is what we use to denote a function. The f is the name of the function, the brackets indicate what the input should be. If we input an x value, what the function gives us is the corresponding yvalue. Therefore, this symbol is also used in place of the y in an equation:
From now on, when we look at the equation of a function, we use f(x) instead of y.
Example: Given the function f(x) = {(1, 2), (3, 5), (4, 6)}, what is the value of f(3)?
Solution: f(3) = 5.
This tells us that when x is 3, y is 5.
Example: Use the given graph to evaluate f(3) and f(-1).
Solution: Looking at the graph, when x = 3, we have y = 4. Therefore the solution is:
Solution: We substitute in 1/2 in place of x.
f(x)
is what we use to denote a function. The f is the name of the function, the brackets indicate what the input should be. If we input an x value, what the function gives us is the corresponding yvalue. Therefore, this symbol is also used in place of the y in an equation:
y = f(x)
From now on, when we look at the equation of a function, we use f(x) instead of y.
Example: Given the function f(x) = {(1, 2), (3, 5), (4, 6)}, what is the value of f(3)?
Solution: f(3) = 5.
This tells us that when x is 3, y is 5.
Example: Use the given graph to evaluate f(3) and f(-1).
Solution: Looking at the graph, when x = 3, we have y = 4. Therefore the solution is:
f(3) = 4
Also from the graph, when x = -1, we have y = 0. Therefore, the solution is:
f(-1) = 0
Example: For the function f(x) = 6x + 3, what is f(1/2)?
Solution: We substitute in 1/2 in place of x.
The solution is f(1/2) = 6.
__________________________________________________________________
Next we talked about domain and range and discussed how to use set notation to write down the Domain and Range of a function.
If the function is given as a set of ordered pairs, we just need to list the values,
Example: What is the domain and range of the following function,
f(x) = {(2, 3) (3,6) (4, 8) (5, 3) (6, 3)}
Solution: D = {2, 3, 4, 5, 6} R = {3, 6, 8}
If we have a graph the domain and range is a bit more tricky.
Example: What is the domain and range of the following function?
Solution: The domain, x, can be any value. In set notation we write this as,
In words, we read this as "The domain is x in the real numbers".
The range, y, can only be positive. In set notation we write this as,
In words we say, "The range is y in the real numbers, such that y is greater than 0."
I then discussed the domain and range of some basic functions:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Homework:
Pg. 22 #1,2, (4-9)eoo, 10, 11, 15c, 16, 17
Pg. 35
#1-5,7,9-11, 13-14





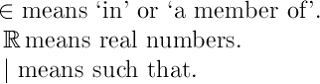
No comments:
Post a Comment